Imagine that the only way to appreciate the beauty of a Ming vase was to shatter it into a thousand pieces, examine the shape and color of each piece, then glue it back together – here’s the hard part – so it’s impossible to detect the seams.

Lin-Wang Wang, Lawrence Berkeley National Lab
This is much like the challenge that faced physicist Lin-Wang Wang and his colleagues at Lawrence Berkeley National Laboratory when they set out to develop physics algorithms to model the nanomaterials equivalent of a Ming vase. The next generation of materials for solar cells and a wide range of electronic components will depend on such solutions.
Wang and his LBNL team – Byounghak Lee, Hongzhang Shan, Zhengji Zhao, Juan Meza, Erich Strohmaier and David Bailey – needed new algorithms to simulate the electronic structure of semiconductor nanomaterials. It is a class of systems so intricate and complex that physicists continue to puzzle over the materials’ unique properties. Because nanomaterials are so tiny – approaching electron wavelengths – they behave very differently from the same material in bulk forms.
Those who study nanostructures are interested mainly in the location and energy level of electrons in the system – information that determines a material’s properties. Unlike uniform systems such as graphite and diamond, Wang’s structures can’t be represented by just a few atoms. Because it is a coordinated system, any attempt to understand the materials’ properties must simulate the system as a whole, Wang says.
A reliable method called density functional theory (DFT) allows physicists to simulate the electronic properties of materials. But DFT calculations are time-consuming and any system with more than 1,000 atoms quickly overwhelms computing resources. The challenge for Wang became to find a way of retaining DFT’s accuracy while performing calculations with tens of thousands of atoms.
Petascale computing, which can distribute calculations over thousands of processor cores, presented a new way to solve large systems like nanostructure calculations. But even at the petascale, calculating a system with tens of thousands of atoms will be extremely challenging because the computational cost of the conventional DFT method scales as the third power of the size of the system. Thus, when a nanostructure size increases 10 times, computing power must increase 1,000 times. Making up that power gap would take the hardware community more than a decade of development. Wang had to find a way to make computational cost scale linearly to the size of nanostructure systems. He settled on a method he calls “divide and conquer,” and it worked like a charm.
It fact, it worked so well that the LBNL team recently won the coveted Gordon Bell Prize, sponsored by the Association for Computing Machinery (ACM), for special achievement in high-performance computing.
“The linear scaling method suddenly makes a big class of problems amenable to simulation,” Wang says.
Oxygen atoms stud the material like raisins in a bowl of oatmeal.
Wang calls his set of new algorithms LS3DF, for linear scaling three-dimensional fragment method. The method’s key lies in the nifty mathematical sleight of hand Wang devised to eliminate evidence of the numerical seams created when the material is divided up and then reassembled.
The program divides the system into numerical squares. It then subdivides the squares into even smaller overlapping squares and rectangles. Once divided, the problem can be easily split up among the thousands of processors available on petascale computing systems. After the calculations are complete the program reassembles the pieces, then performs Wang’s critical step.
“If you do this cleverly, and we have a formula to do this, then the surface of the larger pieces cancels out the surface of the smaller pieces so there will be one core piece left, which just corresponds to the interior of the original system,” Wang says.
This core piece, with artificial seams removed, provides crucial information about the system’s quantum mechanical state, which can then be used to complete the total energy calculation. The program then uses this information to calculate the electrostatic energy of whole system, a much less resource-intensive calculation. The two energy results combine to generate the structure’s total energy and potential.
Being able to remove the artifacts created by dividing up the problem allows large complex systems to be treated like a series of small problems, which is ideal for distributed petascale computing.
The mathematical breakthrough was only the first step to achieving efficient scaling on massively parallel computing systems. Bailey, Shan and Strohmaier of the DOE Office of Science’s Scientific Discovery through Advanced Computing (SciDAC) Performance Engineering Research Institute (PERI) analyzed the algorithms to identify potential performance improvements.
The analysis revealed major roadblocks to achieving peak performance on parallel machines. Many of the programming glitches dealt with how four subroutines communicate and share information. For example, the computational team suggested storing data in memory, rather than storing data on disk, which requires a much more cumbersome and time-consuming method of communication. This change greatly improved scalability and overall performance.
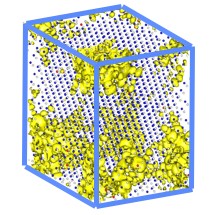
Lawrence Berkeley National Laboratory researchers used the LS3DF program to perform electronic structure calculations for a 3,500-atom zinc-telluride-oxygen alloy. Isosurface plots (yellow) show electron wavefunction squares for the bottom of a conduction band. The small gray dots are zinc atoms, the blue dots are telluride atoms and the red dots are oxygen atoms. The model took one hour to run on 17,000 processors of the Franklin supercomputer at the National Energy Research Scientific Computing Center.
The team performed a series of small test simulations to compare LS3DF’s results to the best DFT programs, such as PARATEC and PEtot. The algorithm produced results that approach the accuracy of DFT. In addition, based on how long it takes PEtot to complete the simulation, the team calculated that LS3DF would be faster with any system larger than 600 atoms.
Armed with a program optimized to parallel computing, Wang and his colleagues chose a real-world problem for a proof of concept. They used LS3DF to test whether a proposed new solar cell material could generate enough electricity to be cost effective. The zinc-telluride-oxygen alloy, first proposed by LBNL, is an oxide that could potentially be less expensive to produce than current solar cell materials. The catch is that similar zinc-telluride semiconductors have proven too inefficient to be practical for solar cells.
The new material included 3 percent oxygen to provide what the materials scientists hope will be a boost to its energy efficiency. The oxygen acts like a stepping stone, allowing electrons excited by solar photons to span an expanse, or “band gap” in the middle of the zinc-telluride, that would otherwise be too wide for many of them to jump. This extra step could increase the material’s energy efficiency from 30 percent to 60 percent.
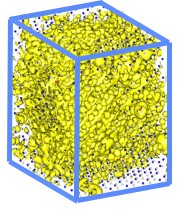
Lawrence Berkeley National Laboratory researchers used the LS3DF program to perform electronic structure calculations for a 3,500-atom zinc-telluride-oxygen alloy. Isosurface plots (yellow) show electron wavefunction squares for the top of an oxygen-induced band. The small gray dots are zinc atoms, the blue dots are telluride atoms and the red dots are oxygen atoms.
The oxygen atoms stud the material like raisins in a bowl of oatmeal, but because there are so few of them and they are randomly scattered, simulating a small portion would miss the raisins. They had to simulate the whole bowl with tens of thousands of atoms. That’s where LS3DF came in.
The team ran the model on Franklin, the 36,864-core Cray XT4 at LBNL’s National Energy Research Scientific Computing Center, achieving 135 teraflops. The initial model, which simulated a 13,824-atom zinc-telluride-oxygen alloy, ran 400 times faster than a similar direct DFT calculation, assuming it were even possible to run such a large problem using the more cumbersome algorithm. In reality, Wang estimated, it would have taken four to six weeks to achieve the same result as LS3DF did in two to three hours.
The initial simulation demonstrated that adding oxygen did in fact provide the atomic stepping stone the researchers hoped it would but with slightly lower efficiency than the best theoretical situation.
“We found that if the percentage of oxygen is small – about 3 percent – there are separate states in the middle of the band gap,” Wang says. “So that indicates this material might be able to be used to generate solar energy.”
Since then, the researchers have run the same problem to test LS3DF’s efficiency on Intrepid, the IBM Blue Gene/P at Argonne National Laboratory. The code achieved 224 teraflops on 163,840 cores – 40 percent of the machine’s peak speed. In a later run on Jaguar, Oak Ridge National Laboratory’s Cray XT5, the code achieved 442 teraflops on 147,456 cores – 33 percent of peak. The ease of moving the program to a new computer system was good news for the research team because they had recently been granted time on Jaguar under DOE’s Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program.
That grant will allow Wang and his team to explore the nature and behavior of new solar cell materials and other nanostructures as never before.
Wang reels off a few of the big questions. “Within an electron field, how do the electrons move? Are they trapped by the surface states or do they move more freely? How do they couple with the photon energy? How does the vibration of the atoms change the electron transport in a nanosystem? All of these questions are not well understood.”
Trial and error can’t address the dynamics of these complex nanostructure systems, Wang says. “To reach that understanding, simulation does play and will continue to play a very important role.”
Understanding the electronic properties of new semiconductor materials may allow researchers to predict how a new nanostructure will behave before actually spending the time and money to make the material. In the case of solar cells, the ability of semiconductor nanomaterials to generate and carry electricity could ease dependence on fossil fuels and generate clean energy, Wang says.
He also is interested in using LS3DF to study the properties of quantum rods and dots. Scientists are already using quantum dots to track the movements of molecules inside living cells. Physicians are enlisting the dots to track tumors, assisting in diagnosis and treatment of cancers. Quantum rods also could be used to create nano-sized electronic devices, and semiconductor materials can transport electricity.
The ability to predict the behavior of new nanomaterials, Wang says, will speed the development of new materials and applications that we can now only dream about.
