Mathematician James Sethian works on the edge. He confronts one of the most challenging problems in physics: capturing the behavior of moving interfaces, the edges where one material pushes into or retreats from another – where a gas mixes and burns, where metals or coatings meet silicon chips, even where ink meets air.
Sethian, a Lawrence Berkeley National Laboratory (LBNL) senior scientist and University of California at Berkeley mathematics professor, has led a three-decade effort to build computer codes that model combustion, that reconstruct the delicate structures hidden in the human body and that improve the analysis of everything from seismic waves to noisy images. The results have, among other practical applications, improved computer chip manufacturing and medical images and helped in oil discovery.
Although most of the applications have moving interfaces in common, their underlying physics and chemistry can vary widely. Sethian has pushed to come up with the right equations to depict those physical and chemical processes, then couple these processes to numerical algorithms that track interfaces.
When he started at Berkeley and LBNL (and for a period at the Courant Institute of Mathematics before returning) in the late 1970s, Sethian focused on building accurate codes to numerically simulate combustion. “The real dynamics of flame fronts are challenging: the geometry of the advancing flame, the local chemistry and complex breaking and merging all factor into determining the efficiency of the burning process,” he says. “I was trying to track the geometry advancing combustion zones, but there weren’t good algorithms to track moving flame fronts in even two dimensions, let alone three dimensions.”
The Level Set Method, can easily handle moving interfaces that change direction, speed and shape.
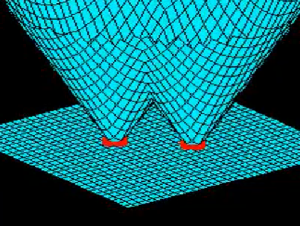
The Level Set Method tracks a moving interface by working with a fixed grid and solving a partial differential equation for the change in distance in the interface from each point on the grid. The method easily tracks twists and turns and direction changes and easily extends to three dimensions.

The Fast Marching Method puts a grid on the moving interface playing field and measures the time and properties of the interface as it crosses each point. It works best on interfaces that move only forward or backward.
Most numerical models of moving interfaces tracked connected “markers” placed along the interface, an arrangement Sethian compares to buoys linked with ropes. The methods either failed or became very difficult if the markers crossed over themselves or the boundary broke up. “That led to trying to build better numerical algorithms to track moving fronts in general,” he says.
One of Sethian’s crucial insights was that computational techniques from gas dynamics and numerical fluid mechanics could be employed to track interfaces of any kind if they were correctly linked in the language of partial differential equations. This meant that a well-established methodology from nonlinear differential equations called numerical hyperbolic conservation laws could be used to handle delicate problems such as the formation of sharp corners and merging fronts.
Sethian’s next step, in collaboration with Stanley Osher at the University of California at Los Angeles, embedded the moving front in a higher dimension. Rather than move markers, the idea is to work on a fixed grid and solve a partial differential equation for the change in the distance in the moving interface from each point on the grid.
Measuring the distance to the moving front, Sethian says, “is considerably easier than riding on top of each twist and turn. It allows the front to break and merge without having to monitor each passing event.” The result, what Sethian calls the Level Set Method, can easily handle moving interfaces that change direction, speed and shape. It’s especially good at capturing unusual twists and turns in the motion and direction of an interface, and it effortlessly extends to three dimensions.
To make these ideas practical and efficient, Sethian introduced the adaptive Narrow Band Level Set Method, developed jointly with David Adalsteinsson, formerly at Berkeley/LBNL and now at the University of North Carolina at Chapel Hill. The method concentrates computational labor in the neighborhood of the advancing interface as it moves, providing extra resolution where all the intricacies occur. Level Set and Narrow Band Level Set methods, now in everyday use around the world, have opened the door to a host of highly complex applications.
Fast Marching Methods, in contrast, work best on problems in which the interface always moves forward or backward without changing direction. These methods put a grid on the playing field and measure the time and properties of the moving interface as it crosses each point. Solving the associated partial differential equation for this “crossing time” is done by rethinking and recasting Dijkstra’s famous method for finding shortest paths on networks into a continuous framework. Sethian’s finite difference Fast Marching Method for front propagation was followed by a class of Ordered Upwind Methods, developed jointly with Alexander Vladimirsky (formerly of Berkeley and LBNL and now at Cornell University). These methods extend Dijkstra-like front propagation techniques to an even wider class of problems, including optimal control and anisotropic front propagation – that is, fronts moving only in one direction. These methods hold onto the Level Set advantage of accurately tracking complex movement and are, Sethian says, stunningly fast.

Dark spots in this electron micrograph cross-section are voids in vapor-deposited material on an etched substrate. This experiment shows remarkable agreement with a simulation created using Level Set and Fast Marching methods.

A simulation of a cross-section of materials vapor-deposited on an etched silicon chip closely resembles actual electron microscope images of a semiconductor.

In this electron microscope image, “trenches” in a semiconductor cross-section have been filled with deposits of conducting material. The dark areas are voids. A computer simulation created using Level Set and Fast Marching methods also found voids created in the deposition process.
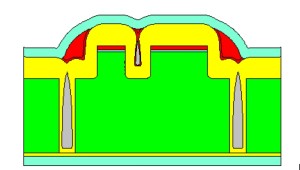
A simulation of a cross-section of materials deposited on an etched silicon chip, with dark voids similar to those found in micrographs.
Researchers across a range of fields have embraced these methods and their variations. A trip Sethian made to Bell Laboratories to address the company’s mathematical and algorithmic research group, for example, led to a long and fruitful exploration of the mechanics of semiconductor manufacturing. The goal was to improve computer chips and microcircuits and lower the cost of production.
Semiconductor manufacturing processes vary, but all involve etching silicon chips, depositing layers or patterns of materials on them, or both. “In all of those models you have to track an interface,” Sethian says. They’re hard problems, he says, because there can be sharp corners, masking and visibility effects that shadow parts of the deposition or etching surface, and unusual chemical and physical processes. For good computer models, the physics and chemistry must be correctly coupled with the interface-tracking techniques.
These algorithms “have allowed process engineers to move interfaces under very complex settings and focus on finding better ways to model the physics and chemistry. This has had an impact on how people simulate semiconductor deposition” and the approach has been adopted worldwide to understand process steps.
Another recent project applies the methods to seismic imaging, a key to finding potential new oil deposits. Geophysicists traditionally try to identify oil reserves by sending sound into the earth and recording the timing and amplitude of the reflected waves. Carefully recording the sound speeds, or seismic velocities, yields pictures of the layers and features below ground.
Producing images from these seismic velocities is done by one of two methods:
- Time migration, which doesn’t work as well if underground features vary greatly from horizontal. It also can be difficult to translate from time coordinates to regular depth coordinates.
- Depth migration, which handles unusual features well but often is based on deriving a seismic velocity model through a series of guesses.
Sethian and colleagues Maria Cameron, formerly at UC-Berkeley and LBNL, now at the Courant Institute, and Sergey Fomel at the University of Texas-Austin developed a series of algorithms that efficiently convert time-migrated image coordinates to depth coordinates and convert migration seismic velocities to depth velocities. The codes, based in part on variations of Fast Marching and Level Set methods, provide a clearer picture of what’s underground.
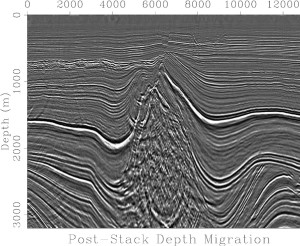
Maria Cameron, Sergey Fomel and James Sethian developed algorithms that can reconstruct depth-migrated images of subsurface features from time-migrated images. This North Sea image shows greater delineations between features than the original.
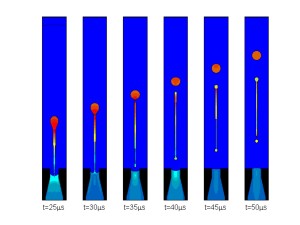
In this numerical-simulation depiction, an inkjet nozzle ejects a “bubble” that’s pinched off and separated from the main body and a residual satellite bubble. The simulation used a combination of Level Set and projection methods to characterize the air-ink boundary, to track movement of the fluid boundaries and to model the surface tension. The simulation compares well with high-speed photographs of inkjets.

Experimental photographs echo simulations of an inkjet ink bubble emerging and separating, followed by the main portion and a residual satellite bubble.
One example shows layers below the North Sea based on time migration coordinates. A salt dome captured by the data is unclear and messy because the method couldn’t cope with the velocity variations. The researchers’ algorithms reconstructed the data in depth coordinates, showing subsurface layers more sharply and clearly than the original image.
Another recent application for Sethian’s algorithms is far from the North Sea but as close as the home office: inkjet printers. The research has widespread implications for workhorse industrial uses ranging from printing integrated circuits and producing LCD and plasma displays to drug testing and microarray production – “advanced processes related to many devices that rely on microfluidics,” Sethian says.
To improve these processes, engineers must better understand what affects the flow, including the nozzle’s shape and wetness, and properties of the material being sprayed. Once again, it’s all about interfaces – in this case, the interface between the material coming out of the nozzle and the air.
One particular issue manufacturers like Epson want to understand is the formation of tail “satellites” – tiny blobs which, as a result of surface tension, break off and trail behind an otherwise smooth flow. The goal is to deeply understand how microjets behave under different fluid conditions, both Newtonian and visco-elastic, and exploit them in new ways. Newtonian fluids such as simple inks have a constant viscosity at a given temperature regardless of shear rate. Visco-elastic fluids, such as pigment-based color inks, will deform and flow under a shear stress, then slowly recover from some of the deformation when the stress is removed. These more complex liquids are challenging parts of industrial processes, biological flows and nanoscale devices.

In this numerical-simulation depiction, an inkjet nozzle ejects a “bubble” that’s pinched off and separated from the main body and a residual satellite bubble. The simulation used a combination of Level Set and projection methods to characterize the air-ink boundary, to track movement of the fluid boundaries and to model the surface tension.
Using a combination of interface methods and highly accurate incompressible fluid flow solvers, Sethian and Jiun-Der Yu at Epson have modeled satellite formation in both Newtonian and visco-elastic ink flowing from a nozzle. Their results strikingly match experimental high-speed images.
Epson has put the algorithms to work, Sethian says. “What we’re trying to do in these applications is to build codes that really model the moving interfaces that arise in engineering devices,” starting with reproducing experimental results and moving on to using simulation to test new configurations. “This is important when you start building things on smaller and smaller scales and vital when you start talking about nanomanufacturing.”
In 2004 the American Mathematical Society and the Society for Industrial and Applied Mathematics awarded Sethian the Norbert Wiener Prize in Applied Mathematics. His work is “a shining example of what applied mathematics can accomplish to benefit science as a whole,” the societies noted. They underscored his pursuit of ideas “from a first formulation of a mathematical model all the way to concrete applications…. His algorithms are currently distributed in widely available packages.”
In 2008, Sethian was elected to the National Academy of Engineering, which recognized his development of efficient methods of tracking moving interfaces.
Sethian, the longtime head of LBNL’s Mathematics Group, continues to both refine and find new applications for his research.
Says Sethian, “The thing I’ve enjoyed most is people’s willingness to invest a lot of time framing the physics, chemistry or biology because they were sure that these methods would ultimately help them.”
